Vector Set for a Tetrahedron with a Base in the x-y Plane and Vertices at Cartesian Coordinates (0,0,0) and (1,0,0)

By

John R. Hoaglund, III

Abstract

Derivation of a vector set for a unit regular tetrahedron resulted in the following four vectors describing the positions of the four vertices relative to the cartesian coordinate system's origin:

Using a vector formula for determining the center of mass of a system of particles, the following center vector describes the position of the center of the tetrahedron relative to the same origin:

The angle of 109.5 degrees between the center of the tetrahedron and any two of its vertices, the tetrahedral bonding angle, is proven with a vector dot product.

Introduction

The geometry of a regular tetrahedron can be determined using vector methods and trigonometry associated with an equilateral triangle which forms all of the four faces of the tetrahedron. Tetrahedrons occur frequently in chemistry and geology. In addition to stable tetrahedral molecules like methane and carbon tetrachloride, the building block of a diamond's unit cell is a tetrahedron because each carbon can covalently bond with 4 other surrounding carbons. Ligands in complex ions, and anions in crystals, assume a tetrahedral configuration around a central cation whenever the coordination number, or crystal coordination number, respectively is 4. A crystal coordination number of 4 is obtained when the ionic radius ratio is in the range 0.228 to 0.414. The ionic radius of Si⁴⁺ is .39 and of O^2- is 1.40 resulting in a cation to anion radius ratio of .278; the shape of the SiO₄^4- anion, the building block of all silicates, is thus a tetrahedron.

Given its importance in science, the tetrahedron's geometry-- the coordinate locations of the four vertices and the center--is determined using vector methods and some trigonometry related to the equilateral triangle that forms the four faces. The resultant vectors are useful for graphically plotting a tetrahedron for many purposes, including x-ray diffraction studies, and physical or computer reconstructive modelling.

Tetrahedron Vertex Vectors

If a tetrahedron with an interfacial side of 1 is placed in the positive xyz quadrant with a vertex, A, at cartesian coordinate (1,0,0) and another vertex, B, at (0,0,0), two of four vertex vectors are readily apparent, namely:

and

If the tetrahedron's position is further restricted such that a third vertex lies in the xy plane as do vertices A and B, the third vertex, C, also has a zero k-component. Furthermore, tetrahedral faces are comprised of equilateral triangles that have 60^o interior angles. Since the ABC face is in the xy plane, the x- and y-component of vector C can be determined with trigonometry applied to the ABC equilateral triangle. Since the BC side (between B at the cartesian origin and vertex C) forms a unit (length = 1) hypotenuse of a 60^o-30^o right triangle, with the 60^o angle located between the BC hypotenuse and the x-axis, the x- and y-components are cos(60^o) and sin(60^o) respectively. The C vector is thus:

It is important to note that the magnitudes of vectors A and C are both 1 (by design, but verifiable), and that the dot product between vectors A and C is ½:

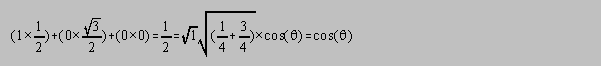
The dot product of ½ implies that the angle between the A and C vector is 60^o. The last vertex, vector D, must also form a 60^o angle, and have a dot product of ½, with vectors A and C (and B if B were not the zero vector). This fact and the fact that the magnitude of vector D must equal 1 enables calculation of the D vector's three components.

Since the A vector has only an i-component of 1, the i-component of D must equal ½:

Using the new D i-component, the D j-component can be determined from the dot product of vector D with vector C because the C k-component is zero eliminating the unknown D k-component from the relation:

The last unknown component, the D k-component, can be determined from the expression for the magnitude of the D vector which must be equal to 1:

The three components make the following vector for D:

Tetrahedron Center Vector

A vector formula from physics for determining the center of mass of a system of particles can be used to determine the center of mass of the tetrahedron if it is assumed that the vertex vectors describe the positions of a system of four particles. The center of mass of a solid corresponds to the center of gravity of the solid if the solid is subjected to a uniform gravitational field (center of mass is defined in terms of mass moments, center of gravity is defined in terms of torques). For an object of uniform density, the center of gravity (or mass) is found at the object's geometric center, specifically the centroid. A tetrahedron's incenter, circumcenter, orthocenter, and centroid all correspond because the angle bisectors, perpendicular bisectors, altitudes, and medians respectively are all the same rays. An excellent discussion of these geometric centers can be found in a geometry lab exercise from Princeton University's computer science department. The answers to the lab (without having to do the exercise) can be found at Swarthmore College's Dr. Math, part of The Math Forum. The vector formula for finding the center of mass of a system of particles is given by a "weighted average" vector:

If it is assumed that the four masses are identical, the center of mass of a system of four particles reduces to an "average" vector:

For the four vertex vectors listed above, the following center vector (origin vector O) describes the position of the origin of the tetrahedron (the center of mass of the tetrahedral system of four identical masses) relative to the same cartesian origin used to describe the vertices:

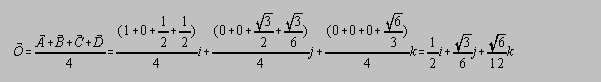
The k-component of O is the perpendicular height of the centroid above the tetrahedron's equilateral triangular face in the xy-plane. The perpendicular from the center of the face to the centroid is the inradius, inscribing a circle tangent to the four faces. The inradius is thus simply the k-component of O:

A segment from the centroid to any of the vertices is an exradius, circumscribing a circle that passes through all four vertices of the tetrahedron. The vertex D, centroid, and inradius share a perpendicular from the xy-plane. The exradius is thus simply the k-component of D minus the inradius, or k-component of O:

An excellent derivation of the inradius and exradius of a tetrahedron using geometry and some trigonometry can be found at caltech's web site on The Platonic Solids: Tetrahedron.

The Tetrahedral Bonding Angle (The O-Si-O Bond Angle)

The angle between the center of the tetrahedron and any two of its vertices, the tetrahedral bonding angle, can be determined with a vector dot product. The angle in question is between two vectors emanating from the tetrahedron's center, formed by subtracting the center vector, O, from the respective vertex vectors. Subtracting center vector O from vertex vector A yields vector AO:

Subtracting center vector O from vertex vector C yields vector CO:

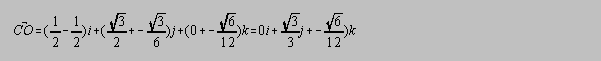
It can be verified that the magnitude of AO equals the magnitude of CO; both are equal to the exradius value above. The exradius value is the bond length, the Si-O bond length, in units equivalent to the interfacial, inter-oxygen, unit distance. A conversion factor for converting both these distances into useful units, like angstroms, can be determined if one of the distances is known (measured). The dot product between AO and CO generates a relation for , the tetrahedral bonding angle:

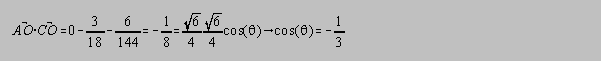
The tetrahedral bonding angle, the O-Si-O bond angle, is therefore: